编译原理

参考： 【编译原理】期末复习 零基础自学_哔哩哔哩_bilibili， 第四章 语法分析和语法分析程序_哔哩哔哩_bilibili

易忘的点

句型句子

短语，简单短语（直接短语），句柄

概述，文法，语言

广义推导和多步推导

句型：可以有终结符也可以有非终结符

句子：只有终结符

求闭包：

问题：求短语，简单短语，句柄

先画语法树，再求所有简单短语，找到最左边的简单短语

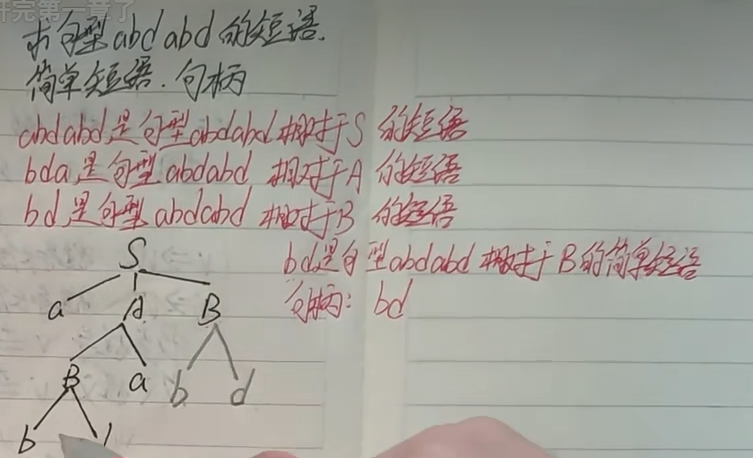
简单短语也称为直接短语

正规式和有穷自动机

正则式

状态转化图

经常有题目给文法让大伙求状态转移图或者状态转移矩阵：

每行的开头是状态，每列的开头是输入条件

然后逐行书写，看每行的状态指出去的状态就行

DFA

五元组

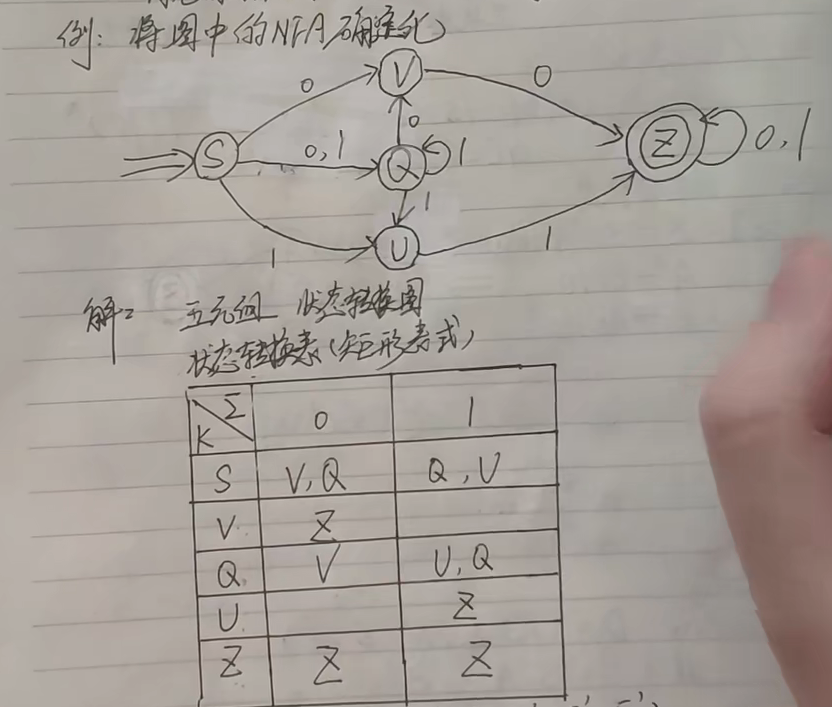
NFA转DFA （无Σ规则）

先根据NFA写出状态转移图，

再根据上面的图写出一个新的高级的状态转移图，每行的行头是状态集合

然后写一下新的S和F, 就是新的开始状态（初态），F是最终状态（表格元素里含有原来NFA最终状态Z的都是F）

题型：把表达式翻译成三地址代码序列

做法：小学换元，逐行写

文法分析

文法的消除回溯、左递归

消除回溯：

提公因式，提到左边，然后右边整个部分换元A'

然后写A‘->xxx

消除左递归：

形如 A->Aα|β，是存在左递归的，把β提取到最左边，然后A->βA', A'->αA’|伊普西隆

语法分析

自上而下的语法分析

First集

定义：找出最左边所有可能出现的终结符

left -> right

分析first集时，看左边

步骤：求First(A)

1）找到最左边是A的，找到其产生式的最左边字符a，如果是终结符那么a∈First(A)

2）找到最左边是A的，找到其产生式的最左边字符a，如果不是终结符则求First(a), (循环这个步骤直到出现1)

当求First(abcAefg)时，等价于求First(a) 加上 假如abcAefg可以多步推导出空串，就加上空串，看个例题

Follow集

left -> right

分析follow集时，看右边所有出现过目标字符的产生式

步骤：求Follow(A)

0）如果 求Afollow集，A是开始符合，直接#

1）如果 V->xAy, y是终结符，则y∈Follow(A)

2）如果V->xAY, Y是非终结符，则First(Y) ∈ Follow(A)

3）如果V->xAY, Y不管是不是终结符，只要可以多步推导出空串，或者遇到V->xA 这种情况，Follow(V) ∈ Follow(A)

SELECT集

求SELECT

LL(1) / 预测分析表 / 输入串分析过程

• 判断LL(1)

对于任意两个非终结符A的产生式（比如A->b和A->c）

若 select(A->b) 和 select(A->c) 没有交集，则是LL(1) 文法

• 消除非LL（1）文法：提取公因子

  

提公因式，换元

• 消除直接左递归

其实相当于把左递归都变成右递归

• 预测分析表 / 求LL(1)分析表

先写出所有的first集和所有的follow集

（其实只需要写出所有产生式右边字符串ABC的first(ABC)）如果遇到空串，则还需要求产生式左边的follow集

根据上面的结果，写LL（1）分析表和字符串栈

举例：

• 输入串的分析过程

初始化表格

开始符 输入字符

然后一直反序压入栈，直到两个都一样，弹出！

自底向上分析

算符优先分析

算符定义

算符优先文法定义

fitstVT

lastVT

算符优先表

逐条分析即可

求短语，句柄，素短语，

根据算符优先表写栈

LR(0)

1拓展文法

2DFS表

3 action goto表

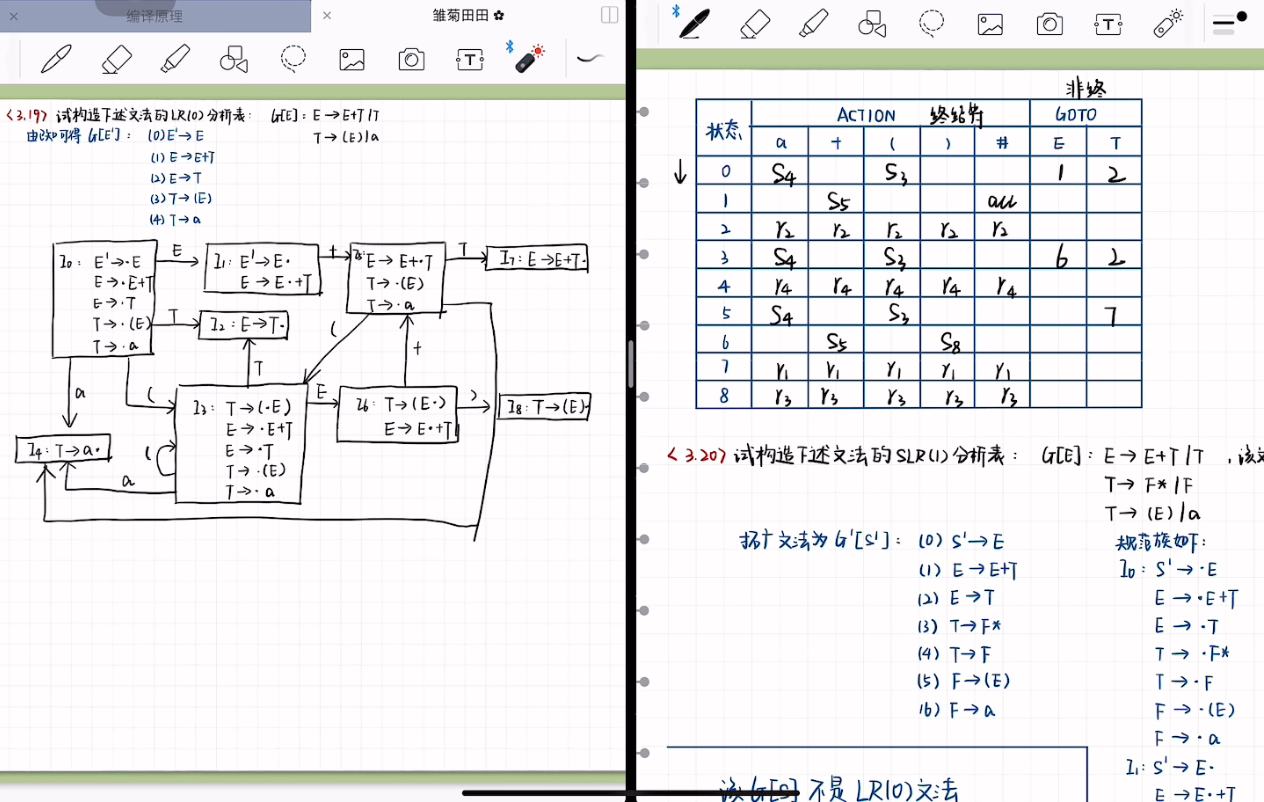
LR(0)文法的判断：没有冲突项目

假如有冲突项目，可以尝试用下面的SLR(1)文法进行优化

SLR(1)

给定一个文法，如何确定它是SLR(1)，并画出相应分析表

步骤：

1.给拓展文法的每个产生式末尾加上#作为终结符，然后求出所有非终结符的follow集

2.写出LR(0)分析表

3.定位到全是rx状态的那行，找到x语句，找到x语句中follow(产生式左边)，只保留该follow集中对应的符号的位置，其余擦掉

4.找到有冲突的所有状态，遍历每个状态，看点后面的终结符∩点后面为空的产生式左边的follow集 == {空集} 若为空集则是SLR(1)

（注意，LR(0) ∈ SLR(1) ，理解为完美的无冲突文法，SLR可以理解为优化后无冲突）

找到冲突（就是在一个状态中，一行的点后面跟着空，另外一行的点仍然后面跟着非空）

LR(1)

在LR(0)分析表加上：

1.写出向前搜索符：

文法开始符，就是默认follow(S‘)={#}，直接就是写为 S'->S,#

随后，逐行求逗号后面的东西，原则是，先看前面的产生式左边X，再去所有产生式中寻找“点后面是X”的产生式A->.Xy

若y是终结符，则直接把y抄下来

若y是非终结符，求first(y)

若没有这个y，（就是A->.X），直接抄这个产生式逗号后面的字符

2.写出类似于LL(1)表的状态转移图，但是每个状态的向前搜索符都要根据当前状态进行修改！

3.画出action-goto表，但是在写rx的那一行，只填写向前搜索符的地方

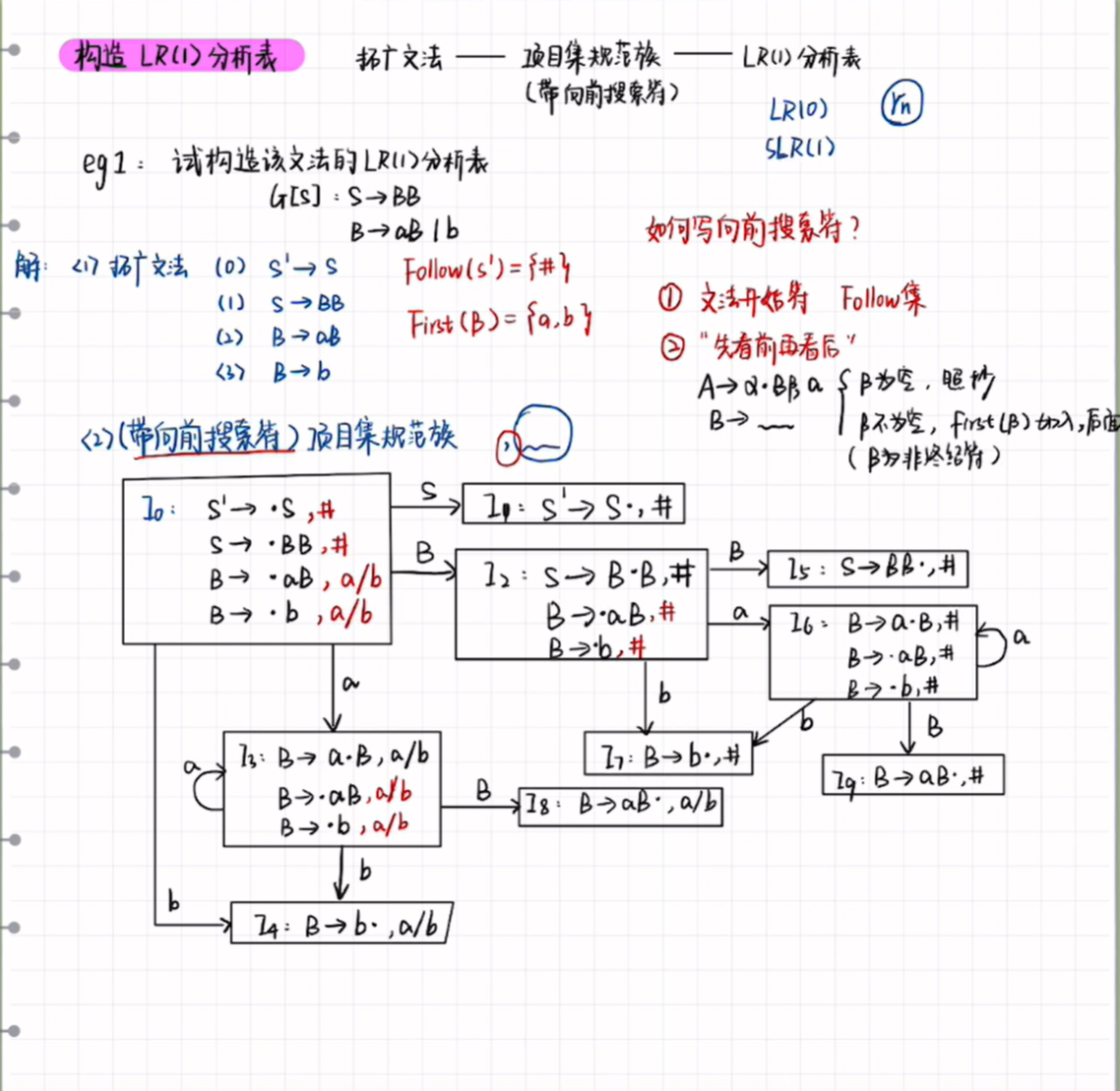
注意它标红的这个地方

判断是否是LR(1):

找到冲突的状态，若 点后面的终结符∩点后面为空那一行的向前搜索符==空集

则是LR(1)

根据LR(1)表写出输入串的分析过程：

初始状态

0

#

然后字符串压入符号栈

当字符串栈和状态栈长度不一样时，查表。如果表中对应的情况是某个状态，则把该状态压入状态栈。如果是rx，就归约，归约注意归约掉几个字符就要弹出几个状态。

重复上述过程直至当字符串栈和状态栈长度一样。

一样时，字符串压入/读取输入字符串第一个字符，然后又重复上面过程

一旦状态转移至acc，过程结束

LALR(1)

就是多求一个同心集（产生式相同，向前搜索集不同），把它像下面一样写在一起当作一个状态

这就比较有意思

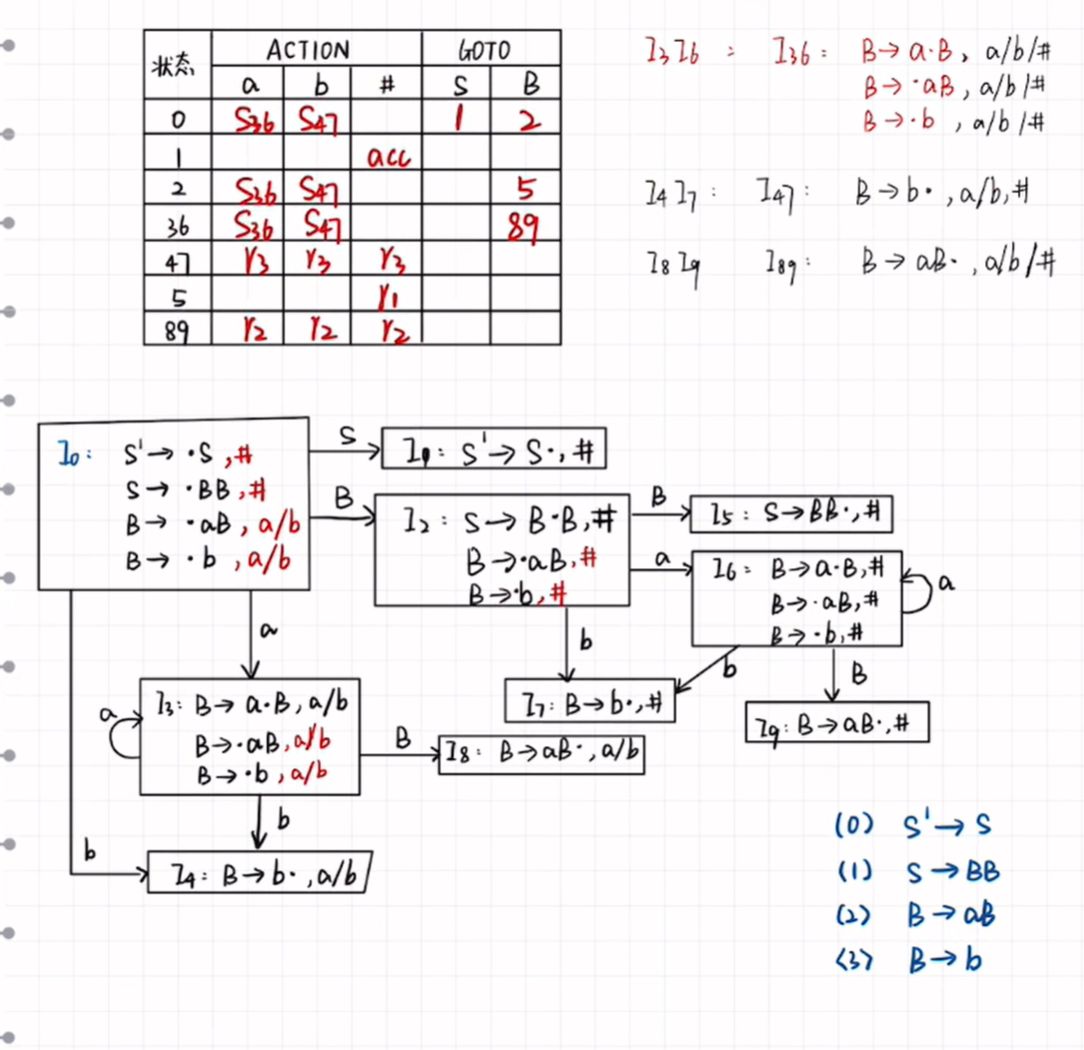
如何知道LR(0), SLR(1), LR(1) 文法

归约项目：（A->a·） 点后面是空

接受项目：（S->a·） 第一个

移进项目： (S->A·ay) 点后面是终结符

待约项目： (S->A·Ay) 点后面是非终结符

LR(0) 无冲突

SLR(1) 有冲突，

LR(1) 有冲突，向前搜索符∩移进项目终结符 == 空集

LALR(1) 有冲突，可以写同心集

例题

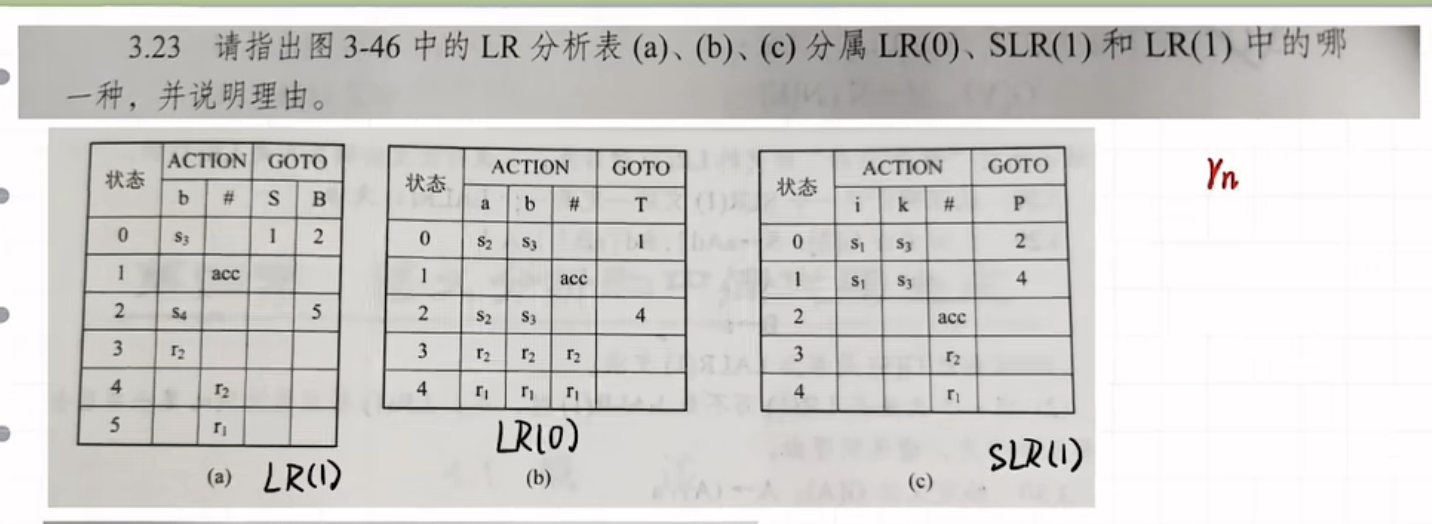
这个只能靠背，LR(1)和SLR(1) 的表的区别是，LR(1)可能两个状态指向同一个rx

给表达式求逆波兰（后缀表示法）

逆波兰：通常把 C=A op B 写成C = AB op的形式，其中等号右边的称为逆波兰式

例题

简单的说就是由外而内的换元，小学换元